ポイント
- 「固体中のワイル粒子」が現れると初めて予言されたスピネル物質について、その有無を検証することに成功しました。
- 先行研究の予言に反し、ワイル粒子は現れない磁性半導体であることを光電子分光実験により明らかにしました。
- 本研究は、新奇な性質の理論予測に潜む難しさと、実験による検証の重要性を示しています。
概要
東京大学 田中 宏明氏(博士課程3年)、広島大学 黒田 健太准教授を中心とする研究グループは、量子科学技術研究開発機構 明石 遼介主幹研究員、東京大学 松田 拓也特別研究員/日本学術振興会特別研究員(当時、現在:特任助教)、松永 隆佑准教授、近藤 猛准教授らと共同で、スピネル(*1)物質HgCr2Se4における電子の振る舞いを解明しました。この物質は、近年注目されている「固体中のワイル粒子」(*2)が現れると理論計算により予言された最初の物質として世界中で注目されてきましたが、10年以上も未解決の問題として残されてきました。本研究で、光電子分光(*3)実験により電子の振る舞いを調べた結果、ワイル粒子は現れない磁性半導体であることを明らかにしました。この結果は先行して行われた理論予測とは一致していませんが、理論計算におけるエネルギーの評価をより精密に行うことで、実験結果と一致する正確な電子の振る舞いを再現することに成功しました。
「固体中のワイル粒子」は、電気的な応答を異様なまでに大きくする要因であることから、ワイル粒子を持つ物質はデバイス応用の観点からも注目されています。しかし、このような性質を持つ物質例は未だに少なく物質探索が強く求められています。本研究で用いた手法は、理論予測の精度を向上させる指針になることが期待されます。また、物質探索において理論や計算により予測するだけでなく実験により検証することの重要性を体現した研究成果であるといえます。
本研究の成果は、米国物理学会が出版する科学雑誌Physical Review Lettersに5月1日にオンライン掲載されました。
論文情報
タイトル:Semiconducting electronic structure of the ferromagnetic spinel HgCr2Se4 revealed by soft-x-ray angle-resolved photoemission spectroscopy
著者:田中 宏明1, A. V. Telegin2, Yu. P. Sukhorukov2, V. A. Golyashov2,O. E. Tereshchenko2, A. N. Lavrov2, 松田 拓也1, 松永 隆佑1, 明石 遼介3,M. Lippmaa1, 新井 陽介1, 出田 真一郎4, 田中 清尚4, 近藤 猛1,黒田 健太5,6(責任著者)
所属:東京大学物性研究所1, ロシア科学アカデミー2, 量子科学技術研究開発機構3,分子科学研究所UVSOR4, 広島大学先進理工系科学研究科5,広島大学WPI-SKCM26
掲載雑誌:Physical Review Letters 130, 186402 (2023).
DOI:10.1103/PhysRevLett.130.186402
背景
固体中の電子は、決まったエネルギーと運動量を持って固体内を運動しています。電子のようなミクロなものを記述する量子力学の法則では、電子の持ちうるエネルギーは運動量ごとに決まっており、また離散的(とびとび)であることを要請します。この関係を図示したのが図1(a)のようなバンド分散であり、バンド分散は固体中の電子の振る舞いを議論する基盤となる重要なものです。
近年では、バンド分散の形状に由来して物質が特異的な性質を有することが分かり、そのような物質の探索が精力的に行われています。その中の一つに、2つのバンドが3次元運動量空間の1点で交わる「ワイル点」があります[図1(a)]。この交点にはプラス・マイナスの符号をつけることができ、その様子が素粒子物理学の「ワイル粒子」に似ていることから「ワイル点」という名前で呼ばれています。ワイル点をフェルミエネルギー(*4)付近に持つ物質は大きな異常ホール効果(*5)を示し、その巨大な応答はデバイス応用の可能性も期待されています。
「固体中のワイル粒子」ともいえるワイル点の存在が初めて理論的に提案されたのが、本研究の対象物質である磁性スピネル HgCr2Se4 [1] です。その後、大きな異常ホール効果などの電子輸送現象を示す物質としてMn3Sn [2] やCo3Sn2S2 [3] が発見され、そのバンド分散にワイル点が存在することがバンド分散の理論計算や光電子分光実験によって確かめられてきました[4, 5]。しかし、HgCr2Se4については、理論的な提案から10年以上経ってもワイル点を実験的に観測したという報告はなされていませんでした。
研究成果の内容
本研究では、SPring-8 BL25SU(*6)とUVSOR BL5Uにおいて HgCr2Se4 に対する光電子分光実験を行い、世界で初めてこの物質のバンド分散を観測することに成功しました。得られたバンド分散には理論的に予測されていたワイル点は現れなかったことから[図1(b), (c)]、予測されたワイル点を有する磁性金属[図1(a)]ではなく、磁性半導体[図1(b)]であることが明らかとなりました。そのため、理論と実験の違いがどこから生まれたのか、議論する必要がありました。
先行研究で行われていたバンド分散の計算は、第一原理計算(*7)と呼ばれる計算手法の一つを用いて行いました。第一原理計算は信頼性の高い計算手法ですが完璧とはいえず、特にエネルギー汎関数(*8)については現在も試行錯誤が重ねられています。先行研究とは異なる精度の高いエネルギー汎関数を用いることで、実験で得られたワイル点を持たないバンド分散を再現することに成功しました[図1(d)]。以上の結果は、ワイル点を持つことが予測されていたHgCr2Se4は実際にはワイル点を持たない物質であるということを実験・計算の両面から実証したといえます。
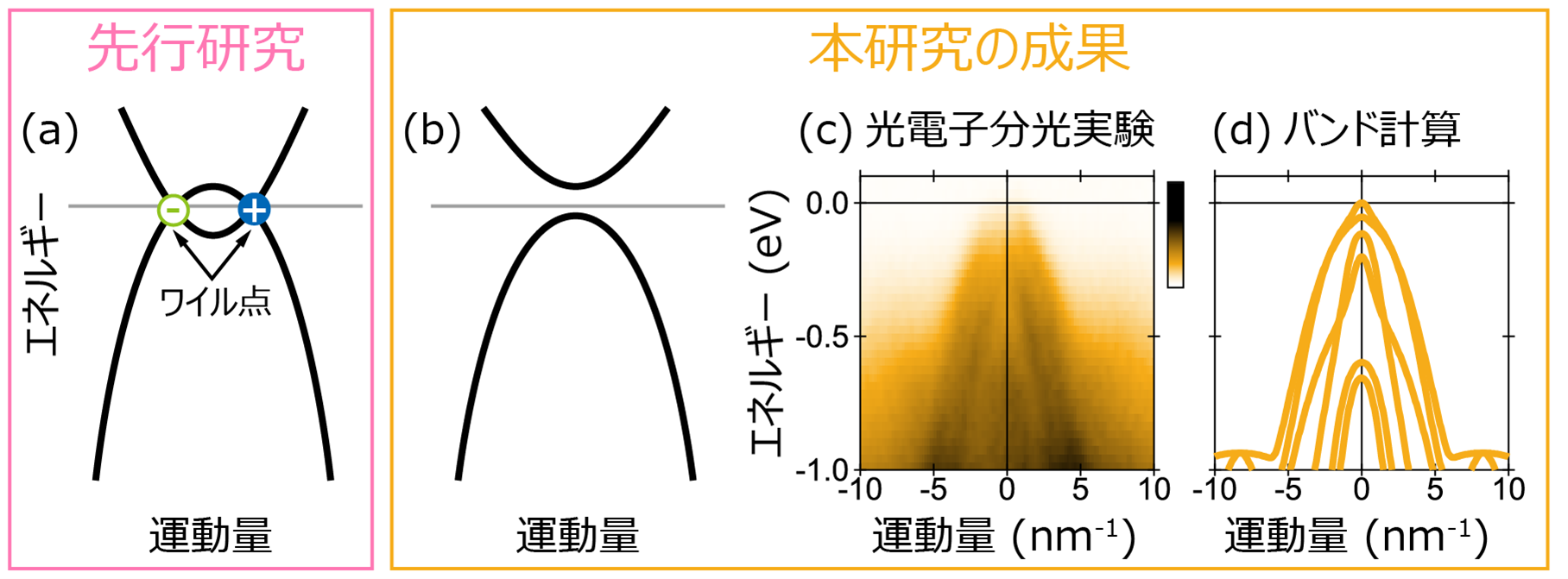
図1: 研究成果の概要。(a) ワイル点を持つバンド分散の模式図。灰色の水平線はフェルミエネルギーを表す。(b) ワイル点を持たないバンド分散の模式図。(c) 光電子分光実験により得られたHgCr2Se4のバンド分散。縦軸のエネルギーはフェルミエネルギーをゼロとしており、単位は電子ボルト(eV)。1電子ボルトは1つの電子を1ボルト持ち上げるのに必要なエネルギーで、1.6×10-19ジュール。(d) 第一原理計算により得られたバンド分散。
今後の展開
本研究は、エネルギー汎関数の選択といった計算条件を適切に設定しなければ電子の振る舞いの予測に失敗してしまう可能性を提示しています。その一方で、実験結果に合致する適切な条件の一例にもなっています。こうした知見を積み重ねていくことで、ワイル点の有無、さらには異常ホール効果などの電気的性質を精度よく予測する方法を確立することができると期待されます。しかし、そのためには計算技術の向上だけではなく、予測を検証する実験技術も欠かせません。 本研究を通じて、理論と実験が両輪となって物理学が発展していく様が改めて浮き彫りになったといえます。
用語解説
*1:スピネル
AB2X4の組成式を持つ鉱物群。
*2:固体中のワイル粒子
固体中の電子が、素粒子物理学のワイル粒子に類似した振る舞いを示している状態。ワイル粒子は,ワイル方程式に従って記述される質量ゼロの相対論的粒子。
*3:光電子分光
光電効果を利用したバンド分散の測定手法。固体試料に対し紫外線またはX線を照射すると、光を吸収した電子が試料表面から光電子として飛び出してくる。光電子のエネルギーと運動量を調べることで、その電子が固体内にいたときのエネルギーと運動量(すなわちバンド分散)を明らかにすることができる。本研究で用いたのは運動量ベクトルの方向も分析する光電子分光測定であり、特に角度分解光電子分光と呼ばれる。
*4:フェルミエネルギー
バンド分散に従いエネルギーの低い方から電子を入れていったときに、最後に入れた(最もエネルギーの高い)電子の持つエネルギーのこと。物質の性質を決定づけるのはフェルミエネルギー付近の電子の振る舞いであるため、特に重要である。
*5:異常ホール効果
ホール効果は、固体に対し電流と磁場を互いに直交するよう印加した際に、それらと垂直に起電力が生じる現象である。これは、電流を生み出している電子の流れが磁場によって曲げられるためと説明される[図2(a)]。磁場がない状態で同じような起電力を生じる現象が異常ホール効果であり、磁場の代わりをするのが運動量空間の仮想磁場である[図2(b)]。ワイル点付近では仮想磁場が発散的に大きくなるため、大きな異常ホール効果が生じると期待される。
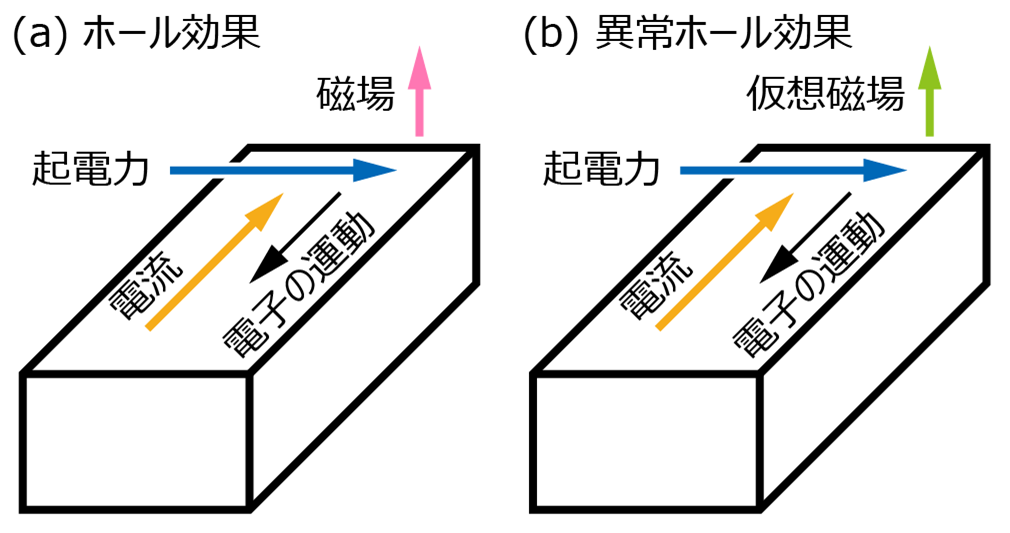
図2: (a)ホール効果・(b)異常ホール効果の模式図。
*6:SPring-8 BL25SU
SPring-8(スプリングエイト)は、兵庫県にある大型放射光施設。放射光とは、光速近くまで加速された電子の運動によって生じる高強度の光のこと。SPring-8では主にX線領域の放射光を発生させ、光電子分光実験のみならず様々な実験・分析に利用している。電子が円運動し放射光を発するリングの周りに多数の実験ブランチが並んだ構造をしており、BL25SUは光電子分光実験を行うブランチの一つ。
*7:第一原理計算
モデル化や人為的パラメータの導入を行わず、物理定数(電子の質量や原子番号など)や客観的な値(原子間距離や結合間の角度など)に基づいて行われる計算のこと。バンド分散の計算においては、密度汎関数理論に基づく第一原理計算が頻繁に利用される。
*8:エネルギー汎関数
密度汎関数理論において、電子の分布からエネルギーを計算する汎関数。電子の分布という座標の関数を引数にとるため、汎関数と呼ばれる。
参考資料
[1] G. Xu et al., Phys. Rev. Lett. 107, 186806 (2011).
[2] S. Nakatsuji et al., Nature 527, 212 (2015).
[3] E. Liu et al., Nat. Phys. 14, 1125 (2018).
[4] K. Kuroda et al., Nat. Mater. 16, 1090 (2017).
[5] D. F. Liu et al., Science 365, 1282 (2019).
