クラスターイオンとは?
クラスターとは、ブドウなどの一房のように、同一のものがひとかたまりになっているものを表します。原子の世界でクラスターといえば、複数の原子が集まって、ひとかたまりになっているものです。例えば、60個の炭素原子でサッカーボールのような形を作っているフラーレンもクラスターの一つです。これをイオン化してMeVエネルギー領域に加速したものをここでは高速クラスターイオンと呼びます。ソフトな弾性衝突に特徴があるeV~keVエネルギー領域のいわゆる低速クラスターイオンに対して、高速クラスターイオンは高密度電子励起を伴う激しい反応を起こすことが特徴で、標的に照射すると2次イオン放出率が高く、高感度な表面分析に応用可能であるなど、新たな量子ビームとして期待されています。
どうやってつくるの?
クラスターイオンを生成するには、いくつかの方法がありますが、TIARAでは、セシウムスパッター型負イオン源を用いて数個から十個程度の負クラスターイオンを作り、タンデム加速器を用いてMeVエネルギーに加速します。また、フリーマンイオン源と400kvイオン注入器の組み合わせでエネルギー500keV程度の2価のフラーレンイオンを生成することもできます。
研究のトピックス
クラスターイオンの生成方法から様々な照射効果までの研究を大学や他の研究機関と協力して行っていますが、ここではクラスターイオンの形が標的との相互作用に及ぼす影響について最近わかったことを御紹介します。
高速クラスターを標的に照射したときに2次イオンが増加することを上述しましたが、この現象がどのようなメカニズムで起こるのかなど、クラスターイオンと物質の相互作用がまだよくわかっていません。これは、歴史ある研究テーマで、現在では、入射ビームが単一イオン(原子一個のイオン)では実験結果をほぼ説明できる相互作用のモデルが確立されています。そこで、高速クラスターイオンと標的との相互作用のモデル構築に資するため、クラスターイオンの構造に着目した実験を行いました。
クラスター特有の作用として、複数の原子がサブナノメートルの微小領域に同時に照射されることにより、物質通過中のクラスター構成原子がバラバラになった後もお互いに影響し合うことが考えられます。したがって、構成原子の空間分布が異なれば、その影響も異なることが予測されます。これを明らかにするために、炭素原子3個からなるクラスターイオンを用いて、影響の違いが現れると考えられる、薄膜を通過させた後の各イオンの電荷を、3個の原子が直線に並んだ場合と三角形に並んだ場合に分けて測定することを試みました。これまでも、クラスターイオンが薄膜を通過した後の平均電荷の測定は行われていましたが、形を選別した測定は初めてでした。そのために、図1に示したクーロン爆発イメージ法に電荷弁別のための平行平板電極及びマイクロチャンネルプレートを組み合わせた実験装置を新たに開発しました。これにより、図2に示すようにクラスターの形とそれを構成しているそれぞれのイオンの電荷を同時に測定することができるようになりました。
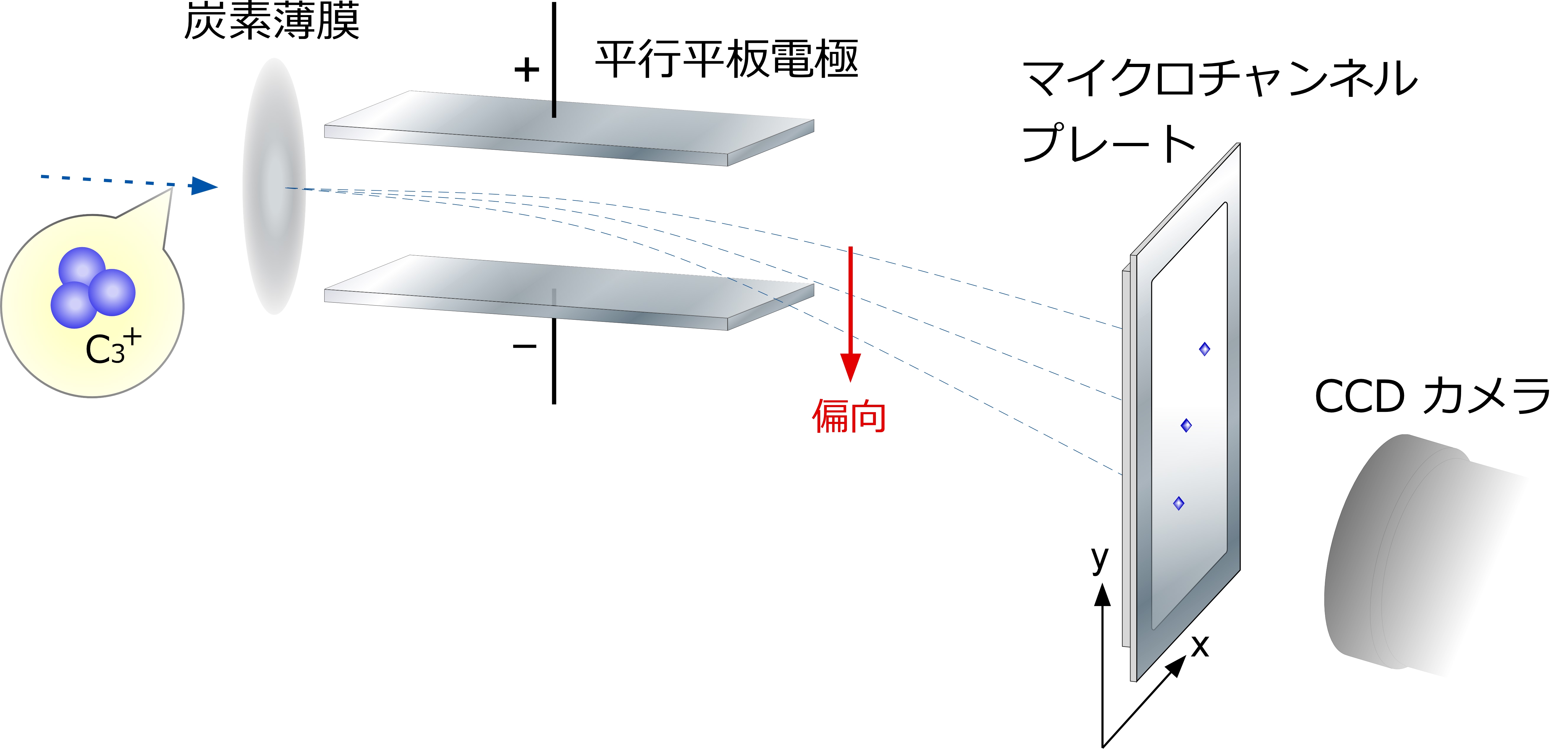
図1 クラスター形状・電荷測定装置
薄膜を通過したクラスターイオンはバラバラのイオンになり、最初の形の情報を残して、各イオンの電荷数に応じて偏向されながらクーロン爆発により広がっていきます。この位置はマイクロチャンネルプレートで検出します。広がった形から、もとのクラスターの形を推測するのがクーロン爆発イメージ法です
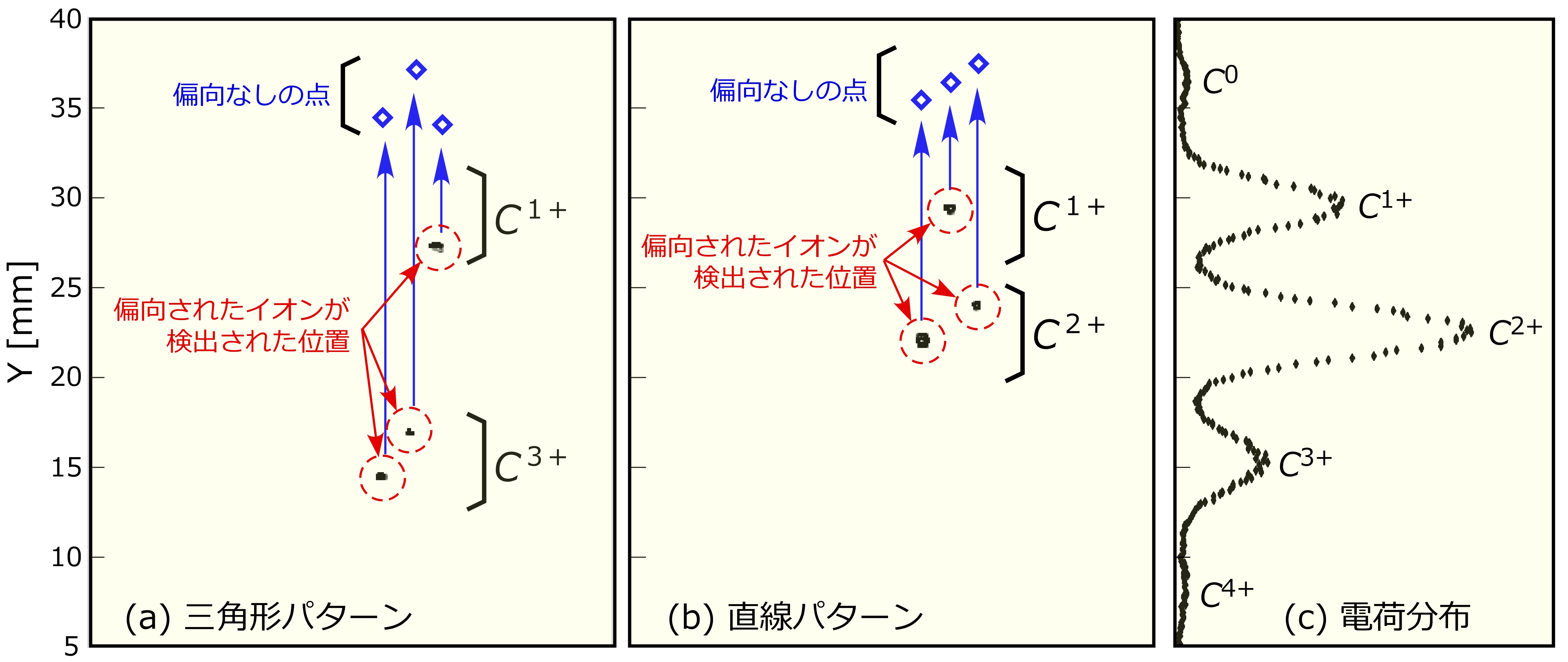
図2 形状の弁別
(a), (b)において赤丸で囲んであるものが実際に検出されたイオンの位置です。この位置でイオンの電荷数が解ります。さらに、平行平板電極にかけた電圧に基づき青で示すもとの形を導出することができます。(a)が三角、(b)が直線の場合になります。(c)は、その場所に来たイオンをすべて足し合わせたものです。
この結果、表1に示すように、平均電荷は直線よりも三角形の方が小さくなり、また、直線状のクラスターの真ん中と両端では真ん中の方が小さくなるということを初めて見出しました。さらに、薄膜通過中にバラバラになった各イオンの外殻電子が残り2つのイオンが作る電場の影響を受けるなど、クラスター構成原子同士の相互作用を取り入れたモデルを作って計算したところ、実験結果と良く一致しました(表1)。これらから、クラスターと標的との相互作用のメカニズムの一端を明らかにすることができました。
| (a) | 直線 | 三角形 | (b) | 中央 | 両端 |
|---|---|---|---|---|---|
| 実験値 | 1.96±0.03 | 1.98±0.02 | 実験値 | 1.86±0.04 | 2.01±0.03 |
| 計算値 | 1.91 | 1.89 | 計算値 | 1.88 | 1.93 |
表1 薄膜通過によりクラスターが解離した後のイオンの平均電荷と計算値
(a)直線と三角形の比較, (b)直線状クラスターの場所による比較
