理論・シミュレーション研究 | スタッフリスト | 相羽 信行

メニュー

• 理論・シミュレーション研究
• 数値トカマク(NEXT)計画
• スタッフリスト
• 論文リスト
• NEXT研究会のお知らせ
• 学生の方へ

氏名：相羽　信行
職制：上席研究員、先進プラズマモデリンググループ、プラズマ理論シミュレーショングループ兼務
住所：311-0193 茨城県那珂市向山801-1

Research Title

• Effects of a Toroidal Rotation on the Stability Boundary of the MHD Modes in the Tokamak Edge Pedestal
• Effect of equilibrium properties on the structure of the edge MHD modes in tokamaks
• Numerical Method for the Stability Analysis of Ideal MHD Modes with a Wide Range of Toroidal Mode Number in Tokamaks
• Effects of 'Sharpness' of the Plasma Cross-Section on the MHD Stability of Tokamak Edge Plasmas
• Analysis of an aspect ratio effect on the stability of external MHD modes in tokamaks with Newcomb equation
• Extension of the Newcomb equation into the vacuum for the stability analysis of tokamak edge plasmas
• Application of the 2-dimensional Newcomb problem in a tokamak
• The Effect of the Aspect Ratio on the External Kink-Ballooning Instability in High-Beta Tokamaks
• Simulation Study on the Motion of the Pressure Perturbation in an Axisymmetric Toroidal System [1]

Effects of a Toroidal Rotation on the Stability Boundary of the MHD Modes in the Tokamak Edge Pedestal

Abstract
Effects of a toroidal rotation are investigated numerically on the stability of the MHD modes in the edge pedestal, which relate to the type-I edge-localized mode (ELM). A new linear MHD stability code MINERVA is developed for solving the Frieman-Rotenberg equation, which is the linear ideal MHD equation with flow. As the result of the stability analysis, it is revealed that the sheared toroidal rotation destabilizes the edge localized MHD modes. The change of the safety factor profile affects this destabilizing effect. This is because the rotation effect on the edge MHD stability becomes stronger as the toroidal mode number of the unstable MHD mode increases, and this toroidal mode number strongly depends on the safety factor profile.

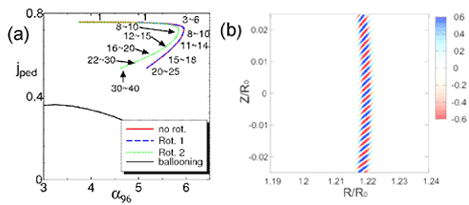
(a) Stability diagram on the (j_ped, α₉₆) plane, where j_ped is the normalized current density near the pedestal, α is the normalized pressure gradient, the subscript 96 means the value at ψ=0.96, where the pressure gradient is steepest. The numbers in this figure shows the toroidal mode number of the MHD modes that determine the stability boundary. (b) Mode structure of the n=500 core ballooning mode in the sheared rotating equilibrium. This is obtained by MINERVA as the benchmarking test.

Reference
[1] N. Aiba, S. Tokuda, M. Furukawa, N. Oyama and T. Ozeki, 22^nd IAEA Fusion Energy Conference, Geneva, Swiss 2008 TH/P9-12.

Effect of equilibrium properties on the structure of the edge MHD modes in tokamaks

Abstract
Effects of the pressure profile and the current density profile inside the top of the pedestal and that of the plasma shape on the expansion of the structure of the unstable edge MHD mode are investigated numerically. The structure of the edge MHD mode is expanded by spreading the envelope of the edge ballooning mode structure due to the increase of the pressure gradient inside the top of the pedestal, and by decreasing the toroidal mode number of the most unstable mode due to the increase of the current density inside the top of the pedestal. In strongly shaped plasmas, the pressure gradient inside the top of the pedestal can approach to the ballooning mode stability boundary and the current density increases enough to reduce the toroidal mode number of the most unstable mode. These increases of the pressure gradient and the current density destabilize the edge MHD mode and expand the structure of this mode.

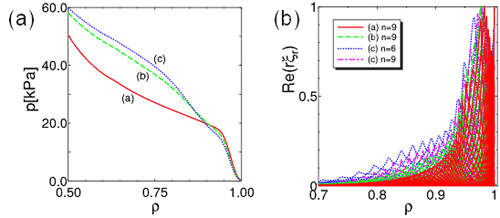
(a) Pressure profiles of the marginally unstable equilibria with different pressure gradient inside the top of the pedestal. (b) Mode structures of the most unstable modes in the different pressure profile equilibria.

Reference
[1] N. Aiba, N. Hayashi, T. Takizuka, S. Tokuda and T. Ozeki, J. Phys.: Conf. Ser. 123, 012008 (2008).

Numerical Method for the Stability Analysis of Ideal MHD Modes with a Wide Range of Toroidal Mode Number in Tokamaks

Abstract
Numerical method for the stability analysis of ideal MHD modes is invented by using the physical model based on the two-dimensional Newcomb equation in combination with the conventional ideal MHD model. The MARG2D code built on this numerical method realizes to analyze the stability of ideal MHD modes with a wide range of the toroidal mode number. The validity of MARG2D has been confirmed by benchmarking tests with the DCON code by identifying the stability boundary of low toroidal mode number MHD modes, and the ELITE code by comparing the growth rates of intermediate to high toroidal mode number MHD modes. With the MARG2D code, the MHD stability property of JT-60SA, the complemental experiment of ITER, is investigated with a focus on the effect of the plasma shape.

Benchmarking results between MARG2D and ELITE[2]. (a) Dependence of the growth rate on the toroidal mode number n. (b) and (c) Mode structures of the eigenfunction of n=10 edge localized MHD mode obtained by MARG2D and ELITE, respectively.

Reference
[1] N. Aiba, S. Tokuda, T. Fujita, T. Ozeki, M.S. Chu, P.B. Snyder and H.R. Wilson, Plasma and Fusion Res. 2, 10 (2007).
[2] P. B. Snyder et al., Phys. Plasmas 9, 2037 (2002).

Effects of 'Sharpness' of the Plasma Cross-Section on the MHD Stability of Tokamak Edge Plasmas

Abstract
Stability of a peeling, a ballooning, and a peeling-ballooning modes, which relate to edge-localized modes (ELMs), are investigated numerically with the linear ideal magnetohydrodynamic (MHD) stability code MARG2D. Effects of 'sharpness' on the stability of the peelingballooning mode are examined, where the sharpness is defined in terms of the curvature at the top or bottom of the outermost flux surface. It is found that the stability limit of the pressure gradient significantly improves as the sharpness increases even when the ellipticity and the triangularity are unchanged. The sharpness is an important parameter for high performance H-mode operations with high pedestal pressure.

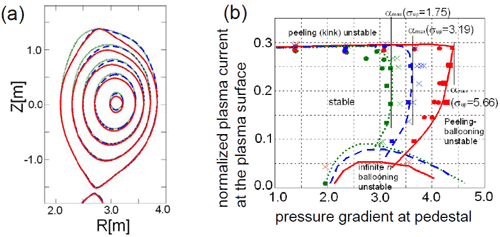
(a) Cross-sections of the equilibria with different sharpness parameters at the top. (b) Stability diagram of the edge localized MHD modes on the (j_edge, alpha) diagram, where j_edge is the normalized plasma current density at the plasma surface, alpha is the normalized pressure gradient at the pedestal.

Reference
[1] N. Aiba, S. Tokuda, T. Takizuka, G. Kurita and T. Ozeki, Nucl. Fusion 47, 364 (2007).

Analysis of an aspect ratio effect on the stability of external MHD modes in tokamaks with Newcomb equation

Abstract
Stability analysis of the external magnetohydrodynamic (MHD) modes is carried out by solving the two-dimensional Newcomb equation. Emphasis is put on an effect of the aspect ratio on the achievable plasma pressure. The decrement of the aspect ratio improves the achievable plasma pressure and increases the toroidal mode number of the external mode restricting the pressure.

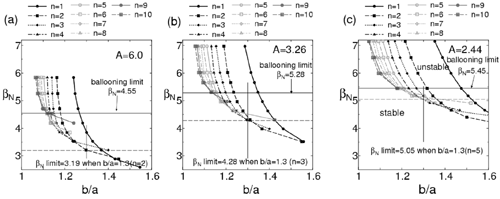
Dependence of the β_N limits on the wall position determined by the stability of 1≤n≤10 MHD modes in (a) A=2.44, (b) 3.26, and (c) 6.00 equilibria.

Reference
[1] N. Aiba, S. Tokuda, T. Ishizawa, J. Plasma Phys. 72, 1127 (2006).

Extension of the Newcomb equation into the vacuum for the stability analysis of tokamak edge plasmas

Abstract
The formulation for solving numerically the twodimensional Newcomb equation has been extended to calculate the vacuum energy integral by using a vector potential method. According to this extension, a stability code MARG2D has been adapted, and coded for parallel computing in order to reduce substantially the CPU time. The MARG2D code enables a fast stability analysis of ideal external MHD modes from low to high toroidal mode numbers on the basis of the single physical model, and then the code works as a powerful tool in an integrated simulation where it is combined with transport codes, and also in the analysis of tokamak edge plasma experiments.

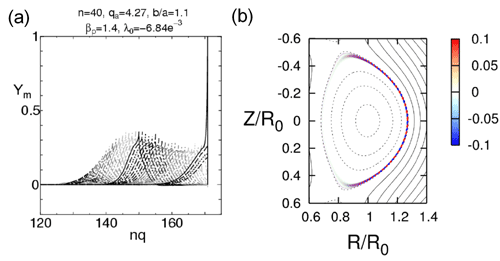
Mode structure of the n=40 edge localized MHD mode obtained by MARG2D in (a) the radial direction and (b) the (R,Z) plane.

Reference
[1] N. Aiba, S. Tokuda, T. Ishizawa and M. Okamoto, Comput. Phys. Commun. 175, 269 (2006).

Application of the 2-dimensional Newcomb problem in a tokamak

Abstract
The theory of the Newcomb equation has been applied to low-n external modes in a tokamak and a method has been developed to compute the stability matrix that gives the change of plasma potential energy due to external modes in terms of the surface values of the perturbations. By using this method, the spectral properties of the ideal external modes has been elucidated, such as coupling between external modes and internal modes, and the difference of the stability properties between a normal shear tokamak and a reversed shear tokamak. These results will be also useful in the stability analysis of resistive wall modes.

Reference
[1] N. Aiba, S. Tokuda, T. Ishizawa and M. Okamoto, Plasma Phys. Control. Fusion 46, 1699 (2004).

The Effect of the Aspect Ratio on the External Kink-Ballooning Instability in High-Beta Tokamaks

Abstract
A theory for the stability analysis of ideal external modes is developed with the property of the Newcomb equation. This theory is also useful for stabilizing resistive wall modes by feedback controls. As an application of this theory, the effect of the aspect ratio on the ideal magnetohydrodynamic (MHD) stability limits of tokamak plasmas are examined numerically. The toroidal mode number n=1 external modes are stabilized by making the aspect ratio smaller.

Reference
[1] N. Aiba, S. Tokuda, T. Ishizawa and M. Okamoto, J. Plasma Fusion Res. SERIES Vol. 6, 241-244 (2004).

Simulation Study on the Motion of the Pressure Perturbation in an Axisymmetric Toroidal System [1]

Abstract
In tokamaks, it is observed that an ablated and ionized pellet moves toward the low field side of the torus. This phenomenon can be considered as the Magneto- HydroDynamic (MHD) wave propagation in the 1/R varying toroidal field because the pressure perturbation is induced by injecting a pellet, where R is the major radius of tokamaks. The dominant mechanism which causes this displacement is revealed, by solving nonlinear MHD equations numerically, as the multi-dimensional nonlinear fast magnetosonic wave propagation in a toroidal magnetic field. Linear wave propagation does not work for this displacement. The nonlinearity is clarified by successive approximation.

Reference
[1] N. Aiba, S. Tokuda, T. Hayashi and M. Wakatani, J. Phys. Soc. Jpn. 73, 364-373 (2004).