プラズマ理論シミュレーショングループ
氏名:宮戸 直亮
職制:上席研究員、BA計画調整グループ、プラズマ理論シミュレーショングループ兼務
住所:039-3212 青森県上北郡六ヶ所村大字尾駮字表舘2-166
Research Title
- Push-forward representations in the standard gyrokinetic model
- Extension of the standard gyrokinetic model
- Fluid moments in modified guiding-centre coordinates
- A modification of the guiding-centre fundamental 1-form with strong ExB flow
- Simulation study for turbulent transport in tokamak plasmas
- Interaction between zonal flows and Itg turbulence in tokamaks
- Nonlocal behaviour of zonal flows in tokamaks
Push-forward representations in the standard gyrokinetic model
Abstract
Two representations of fluid moments in terms of a gyro-center distribution function and gyrocenter coordinates, which are called push-forward representations, are compared in the standard electrostatic gyrokinetic model. In the representation conventionally used to derive the gyrokinetic Poisson equation, the pull-back transformation of the gyro-center distribution function contains effects of the gyro-center transformation and therefore electrostatic potential fluctuations, which is described by the Poisson brackets between the distribution function and scalar functions generating the gyro-center transformation. Usually, only the lowest order solution of the generating function at first order is considered to explicitly derive the gyrokinetic Poisson equation. This is true in explicitly deriving representations of scalar fluid moments with polarization terms. One also recovers the particle diamagnetic flux at this order because it is associated with the guiding-center transformation.
However, higher-order solutions are needed to derive finite Larmor radius terms of particle flux including the polarization drift flux from the conventional representation. On the other hand, the lowest order solution is sufficient for the other representation, in which the gyro-center transformation part is combined with the guiding-center one and the pull-back transformation of the distribution function does not appear.
Reference
[1] “On push-forward representations in the standard gyrokinetic model,” N. Miyato, M. Yagi and B. D. Scott, Physics of Plasmas 22, 012103 (2015).
Extension of the standard gyrokinetic model
Abstract
The standard gyrokinetic model is formulated for perturbations with short wavelength and small amplitude (gyrokinetic ordering). Therefore, there is no reason that the standard model is valid in regimes beyond the gyrokinetic ordering. We consider two regimes beyond the gyrokinetic ordering:
1) Strong flow regime
2) Long wavelength (but weak flow) regime
It is found that the standard model is not always valid in regimes beyond the gyrokinetic ordering and modifications to the standard model are needed. The key of modifications is a higher order term in the guiding-centre transformation which is not considered in the standard model. Considering the higher order term gives additional terms in the gyrokinetic Hamiltonian and in the gyrokinetic quasi-neutrality condition.
Reference
[1] "On the gyrokinetic model in long wavelength regime,” N. Miyato, B. D. Scott and M. Yagi, Plasma Phys. Control. Fusion 55, 074011 (2013).
[2] “Gyrokinetic model beyond the standard ordering,” N. Miyato, Contrib. Plasma Phys. 56, 543 (2016).
Fluid moments in modified guiding-centre coordinates
Abstract
A general fluid moment in the particle coordinates is represented in terms of fluid moments in modified guiding-centre coordinates with strong ExB flow derived by the phase space Lagrangian Lie-transform method. It is called the push-forward representation of the particle fluid moment associated with the guiding-centre transformation. The representation derived is similar to that in terms of gyro-fluid moments in the standard gyrokinetic theory in the long wavelength limit. Since the particle coordinates are transformed to gyro-centre coordinates by the two-step transformation in the standard gyrokinetic formulation, two exact push-forward representations are possible. Although the exact representation usually used in the standard gyrokinetic theory has a different form from that in the modified guiding-centre case, the correspondence between the two cases is shown more clearly by considering the alternative form of the push-forward representation for the standard gyrokinetic case.
Reference
[1] "Fluid moments in modified guiding-centre coordinates," N. Miyato, B. D. Scott and S. Tokuda, J. Plasma Fusion Res. Series 9, 546 (2010).
[2] "Fluid moments in the reduced model for plasmas with large flow velocity," N. Miyato and B. D. Scott, Plasma and Fusion Research 6, 1403147 (2011).
A modification of the guiding-centre fundamental 1-form with strong ExB flow
Abstract
A modified guiding-centre fundamental 1-form with strong ExB flow is derived by the phase space Lagrangian Lie perturbation method. Since the symplectic part of the derived 1-form is the same as the standard one without the strong ExB flow, it yields the standard Lagrange and Poisson brackets. Therefore the guiding-centre Hamilton equations keep their general form even when temporal evolution of the ExB flow is allowed. Compensation of keeping the standard symplectic structure is paid by complication of the guiding-centre Hamiltonian. However it is possible to simplify the Hamiltonian in well localised transport barrier regions like a tokamak H-mode edge and an internal transport barrier in a reversed shear tokamak. The guiding-centre Vlasov and Poisson equations are derived from the variational principle. The conserved energy of the system is obtained from the Noether's theorem.
- A modified guiding-centre 1-form with Exb flow,
with a guiding-centre Hamiltonian,
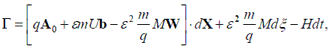
where D is the Exb drift velocity.
Reference
[1] "A Modification of the Guiding-Centre Fundamental 1-form with Strong ExB Flow," N. Miyato, B. D. Scott, D. Strintzi, and S. Tokuda, J. Phys. Soc. Jpn. 78, 104501 (2009).
Simulation study for turbulent transport in tokamak plasmas
Abstract
The main topic of the research is to clarify the nonlinear interaction between zonal flows and drift wave turbulence including ion temperature gradient (ITG) driven turbulence. It is investigated by global Landau-fluid simulations.
Reference
[1] N. Miyato et al., Journal of Plasma Physics 72, 821-824 (2006).
[2] N. Miyato et al., Nuclear Fusion 47, 929-935 (2007).
[3] “Effect of ion temperature gradient driven turbulence on the edge-core connection for transient edge temperature sink,” N. Miyato, Plasma Fus. Res. 9, 1203148 (2014).
Interaction between zonal flows and Itg turbulence in tokamaks
Abstract
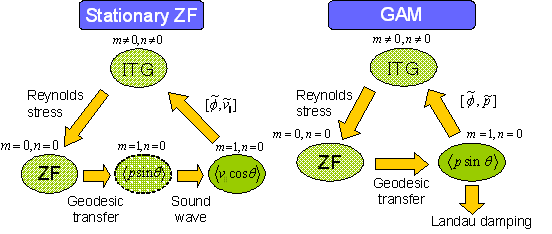
Two kinds of zonal flows (ZFs) are possible in tokamak plasmas. One is almost stationary ZF and the other is oscillatory ZF called geodesic acoustic mode (GAM). The diagrams below show energy loop between ITG turbulence and ZFs in a quasi steady state.
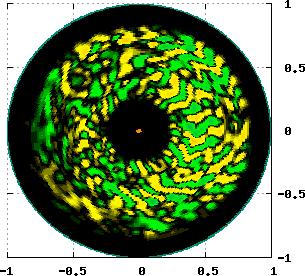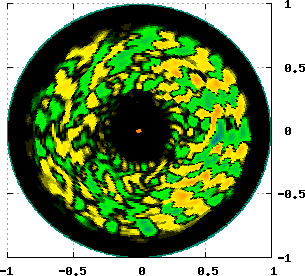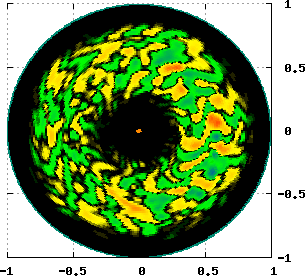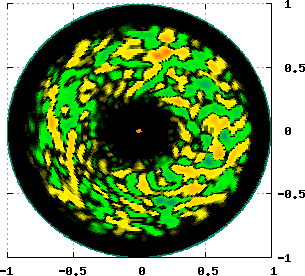
Reference
[1] N. Miyato et al., Physics of Plasmas 11, 5557-5564 (2004).
[2] N. Miyato et al., Nuclear Fusion 45, 425-430 (2005).
Nonlocal behaviour of zonal flows in tokamaks
Abstract
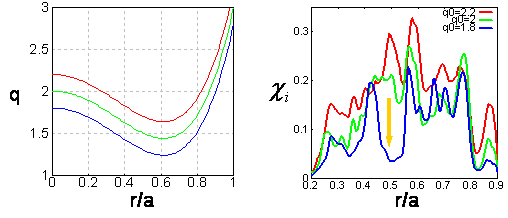
Oscillatory ZFs called geodesic acoustic modes (GAMs) show nonlocal behaviour in their frequency. The radial width in which the GAMs have the same frequency is almost proportional to the geometric mean of an ion Larmor radius and a plasma minor radius.
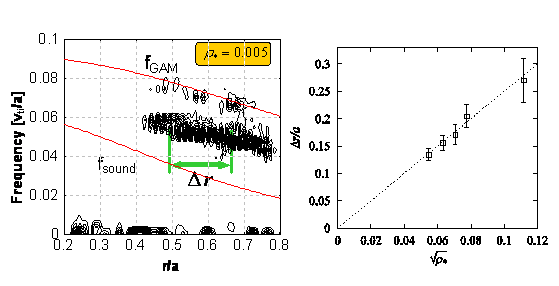
Reference
[1] N. Miyato et al., Plasma Phys. Control. Fusion 48, A335-A340 (2006).

